DeepWater Buoyancy collaborated with Maine Marine Composites (MMC) on a paper for the Oceans18 Conference.
The paper, entitled “A Design of Experiments based approach to engineering a robust mooring system for a submerged ADCP”, was presented by Tobias Dewhurst, PhD of MMC.
A copy of the paper can be downloaded HERE.
A copy of the PowerPoint presentation can be downloaded HERE
A Design of Experiments Based Approach to Engineering a Robust Mooring System for a Submerged ADCP
Authors
Michael T. MacNicoll, Tobias Dewhurst, PhD, Richard Akers, P.E. – Maine Marine Composites LLC, Portland, ME, USA
David A. Capotosto, DeepWater Buoyancy, Inc., Biddeford, ME, USA
Summary
A model-based engineering approach was used to design an optimal single-point mooring for a subsea Acoustic Doppler Current Profiler (ADCP). Numerous inputs and criteria were considered. Target deployment depth, environmental conditions, and seafloor characteristics were identified for the selected site in the Gulf of Maine. Design variables included buoy shape, buoy volume, gravity anchor mass, chain size, acoustic release buoyancy, and wire rope diameter. Design criteria included wire rope safety factor, chain load safety factor, ADCP pitch, ADCP knockover (set down), anchor sliding, and the recoverability of the Acoustic Release. A design methodology based on Design of Experiments (DoE) theory was used to develop a mooring system that satisfied all the competing design objectives while minimizing cost. This methodology limited expensive simulation time while resulting in a satisfactory mooring design.
Keywords—Acoustic Doppler Current Profiler; ADCP; Mooring Design; Design of Experiments
I. Introduction
A. Motivation
Numerous competing criteria must be considered when designing mooring systems for oceanographic instruments. These criteria include the deployment depth range, acceptable pitch angles, and cost. Furthermore, environmental conditions and seafloor characteristics must be accounted for properly. An under-designed system could allow excessive instrument motion or movement of the anchor. An overdesigned system increases component costs and requirements for deployment assets. For example, oversizing the mooring line adds weight to the system, which in turn increases the buoyancy requirement. Increasing the buoyancy creates greater stress on the mooring line and increases the anchor weight requirement. These changes drive up the costs. A successful design approach must balance multiple competing criteria without requiring excessive simulation time, while resulting in a mooring system that meets the design criteria under all expected environmental conditions without overdesigning the system.
B. Methodology
A simulation-based engineering approach was used to design an optimal single-point mooring for a subsea Acoustic Doppler Current Profiler (ADCP). This approach satisfied the objectives above by applying computer simulations in a Design of Experiments (DoE) framework. Using the DoE methodology, an experiment was designed to identify the factors that drive mooring system performance and cost. The results of the experiment were then used to optimize the system based on linear regression of the DoE results. This regression model accounted for both the first-order interactions between factors, and the competing design objectives discussed above.
Simple experiments often attempt to isolate variables and study their effects on a system one at a time. There are two limitations with this approach. First, the number of variables is artificially limited, to limit the time and effort to carry out an experiment. Second, this approach fails to study how design factors might interact with each other. The Design of Experiments (DoE) approach overcomes these shortcomings [1].
DoE is a systematic approach to quantify how sensitive a system is to factors that are believed to influence that system. A DoE setup will require first identifying the factors to be examined. Next, two levels are selected for each factor, and experiments are carried out on the system. This can be done using each possible combination of levels and factors, or a subset of each combination. When the number of factors is large, then the number of all possible combinations of levels and factors can become excessive, so a fractional factorial experiment may be designed that still ensures there is no aliasing between factors and first order interactions between factors.
In the present study, MMC applied a DoE approach to design a mooring system for a submerged ADCP. The DoE approach allowed for efficient examination of a very large design space, identification of the design factors that have the greatest impact on the design objectives, and development of an optimal design.
Fig. 1 lays out this design approach. An initial design is proposed, and design constraints are quantified. Design factors are identified. Upper and lower levels are determined for each factor. These levels represent the highest and lowest likely values for each design factor. Next, a DoE experiment is set up and computer simulations are run. The results of the DoE simulations are used to develop a regression model based on the design constraints. If the optimal design does not satisfy the design constraints, a revised DoE is developed. The revised DoE will require adjusting the levels of the factors, or adding new factors, to improve the results. The process is repeated until the optimal design converges on one which satisfies the constrained design objectives.
Figure 1. Flowchart of Design Approach
II. Procedure
A. Mooring System Initial Design
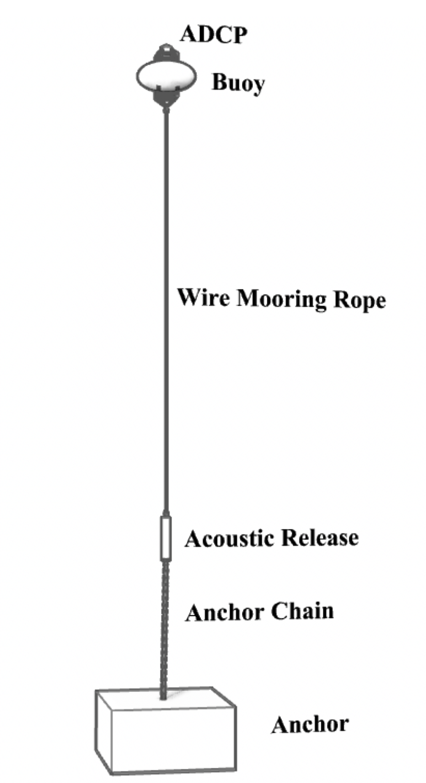
The ADCP mooring equipment was based on a typical mooring system design (see [2] for example) The arrangement consists of an anchor, connected with chain to an acoustic release (used to retrieve the ADCP) with some added buoyancy, and a wire rope from the acoustic release to a buoy that keeps the ADCP in position. The ADCP is attached to the top of the buoy and is positioned 100 meters below the surface to avoid the most extreme wave motions. The buoy has the dual objectives of (1) providing reserve buoyancy to keep the ADCP upright and in position to minimize pitching and knockover (set down) motions, and (2) to bring the mooring string to the surface when the release is activated. The arrangement is shown in Fig. 2.
Figure 2 Components of moored ADCP. Chain and wire rope lengths are not to scale.
B. Environmental Conditions
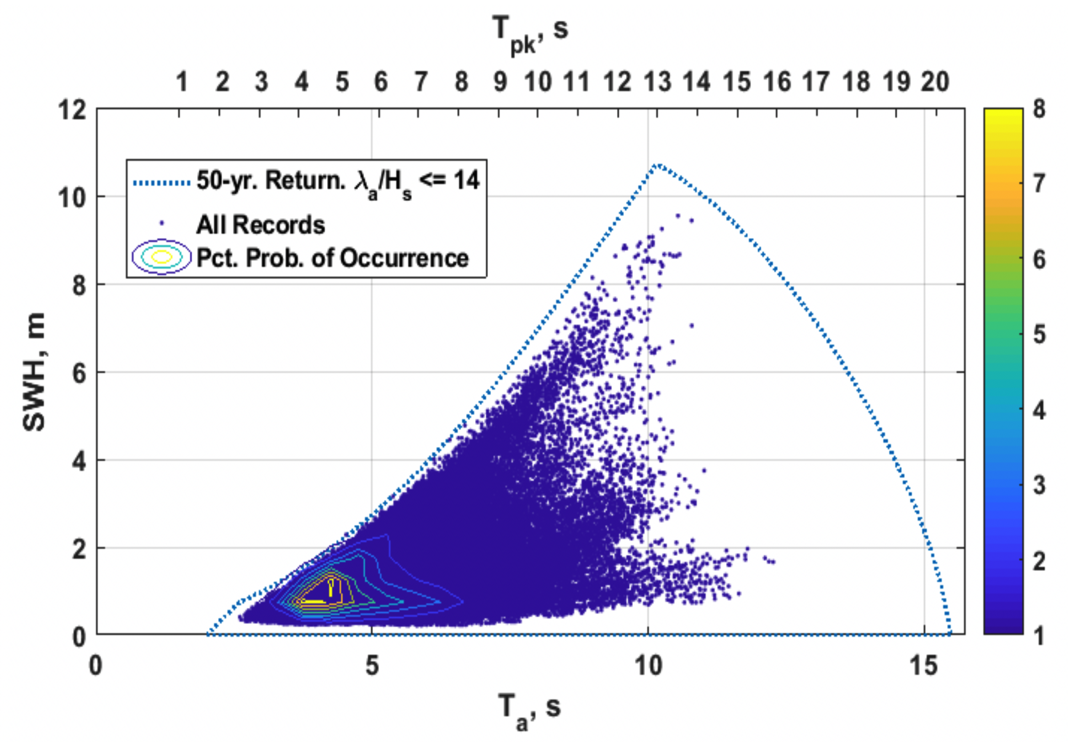
The ADCP will be deployed near the National Oceanic and Atmospheric Administration’s (NOAA) National Data Buoy Center (NDBC) Station 44098, Jeffrey’s Ledge in 300 meters of water [3]. A robust metocean study of the deployment location was performed by MMC using historical wave data from NDBC for the years 2008-2015. This study used Principle Component Analysis and the inverse first-order reliability method (I-FORM), as described in [4] and as implemented in the Wave-Energy-Converter Design Response Toolkit [5]. In this approach, linear algebraic methods are used to develop an orthogonal basis whose components are aligned so as to represent the largest degree of variance. Once these principal components are identified, extreme contours are generated using the I-FORM approach [6]. The extreme contour was limited to the steepness at which waves generally break. The resulting 50-year return period contour is shown in Fig. 3. From this analysis, the largest 50-year return period significant wave height is 10.7 m, with a peak period of 13 s.
Figure 3 50-year sea state contour at Jeffrey’s Ledge, NH (solid blue line). Blue dots are historical observations. Contour lines show probabilities of occurrence.
C. Design Constraints
As the goal of this study was to use a DoE-based approach to design a robust and cost-effective mooring system, the following seven design objectives were identified:
- Prevent uplift and sliding of the anchor
- Minimize knockover of the ADCP
- Minimize pitch of the ADCP
- Maintain minimum safety factor of the wire rope of at least 1.67 [7]
- Maintain minimum safety factor of the anchor chain of at least 1.67 [7]
- Acoustic release must have enough buoyancy to be recoverable if the wire rope fails and the acoustic release is disconnected from the upper buoy.
- Minimize the cost of the system
D. Design Factors
Six design factors were identified. These are the variables of the mooring arrangement that will be tuned by the DoE simulations. Two factors related to the ADCP buoy. Two buoy shapes, a spherical buoy and an elliptical buoy, were simulated. These are based on ADCP buoys made by DeepWater Buoyancy Inc., shown in Fig. 4. In addition, two buoy volumes (and corresponding buoyancy lift forces) were simulated for each shape. The buoy has the primary objectives of mitigating ADCP pitching and knockover. Larger buoys will increase the cost of the system and the loads on the mooring lines, while smaller buoys will be less effective in mitigating ADCP motions.
The third design factor is the mass of the anchor. The anchor must be heavy enough that it does not move, either vertically or laterally. However larger anchors will increase the cost of the system.
The diameter of the chain and wire rope components of the mooring line are the next two factors. The primary trade-off for these components is safety factor vs. cost. Smaller components will have lower safety factors, but larger components will drive up the cost of the system.
The final factor is the buoyancy of the acoustic release. This must provide enough uplift to ensure that the acoustic release can be recovered if the wire rope fails and the acoustic release is separated from the reserve buoyancy.
These design factors, and the corresponding higher and lower levels, are summarized in TABLE I. In a full factorial DoE, every combination of high and low levels for each factor would be simulated, resulting in 27=128 simulations. In this work a fractional factorial matrix was design with resolution four, which ensured that all primary factor and first order interaction effects could be isolated without aliasing, while reducing the number of required simulations [8].
Figure 4 ADCP buoyancy options. Top: spherical buoy; bottom: elliptical buoy (source: www.deepwaterbuoyancy.com).
Table 1 Summary of DoE Input Factors
E. Computer Simulation
A computer simulation of the ADCP and its mooring system was developed using the commercial software OrcaFlex by Orcina [9]. Simulations were run for each row of the fractional factorial matrix during the 50-year return period storm with a steady current.
Three phases of ADCP deployment were investigated in the DoE simulations, including (1) deployment in calm water, (2) survival in 50-year return period storm event, and (3) retrieval using the acoustic release. Deployment involved releasing the ADCP from the surface and allowing the entire system to sink until the anchor reached the seabed. The retrieval was simulated by disconnecting the reserve buoyancy buoy from the wire rope, and the acoustic release from the chain. The acoustic release, provided it was buoyant enough, would rise to the surface with the wire rope.
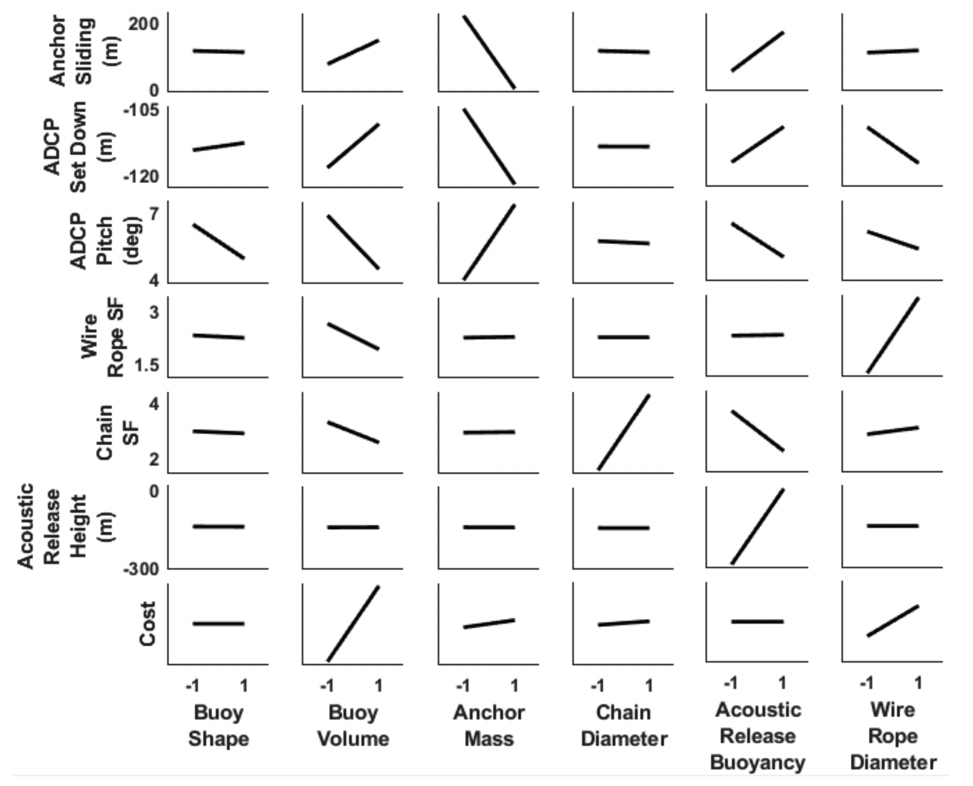
The results of the DoE simulations are shown in Main Effects plots in Fig. 5. Each subplot shows the sensitivity of a single factor to the corresponding design objective. The steeper the line, the more sensitive the objective is to that factor. Some of the design trade-offs that must be considered are shown clearly in this figure. For example, increasing the buoy volume has the beneficial effects of decreasing the ADCP pitching and set down. However, there are also negative consequences to increasing the buoy volume, such as increasing the mooring loads, increasing the likelihood of anchor sliding, and increasing the cost of the system. To weight the pros and cons of conflicting design objectives, a global objective function was developed. This is discussed in the following section.
Figure 5 Summary of Design of Experiments simulation results. Each row shows the Main Effects plots for every factor and a single objective. Each column shows the Main Effects plots for every objective for a single factor.
F. Optimization Results
The results of the DoE simulations were used to optimize the ADCP mooring system design. For each of the design objectives discussed above, a linear regression model was computed. For objective i, this takes the form:
![]() (1)
(1)
Here bi are the regression coefficients and X are the levels for each factor, including first-order interactions and a constant intercept.
There are several limitations with using a strictly linear regression model to optimize the mooring design. First, there is no convenient way look at multiple design objectives at the same time. Second, many objectives are not linear. For example, the safety factor of the mooring rope must be at least 1.67, however, once it is over that threshold, it is less critical that it continue to be improved. To account for these limitations, each design objective was normalized with a logistic function,
![]() (2)
(2)
Here fi(X) is the regression function for objective, i, and ki and x0,i are steepness and midpoint parameters which must be identified. The global objective function is then taken as the minimum of each objective:
![]() (3)
(3)
This is illustrated in Fig. 6. The wire rope safety factor experiences a steep drop-off when the safety factor approaches the design target. Above the target, the safety factor is not as sensitive to changes in the wire rope diameter. The cost objective function does not experience a steep drop-off, as there is no hard target. The optimal wire rope diameter is the peak of the Combined Objective function, which is located at the intersection of the two sub-objectives.
Figure 6 Illustration of wire rope safety factor and cost objectives as a function of wire rope level. The combined objective function is shown in red.
When all six design factors and all seven design objectives are considered, it is not possible to visualize the objective function in two dimensions. Fig. 7, Fig. 8, and Fig. 9 each show the objective function plotted as a surface plot for two factors.
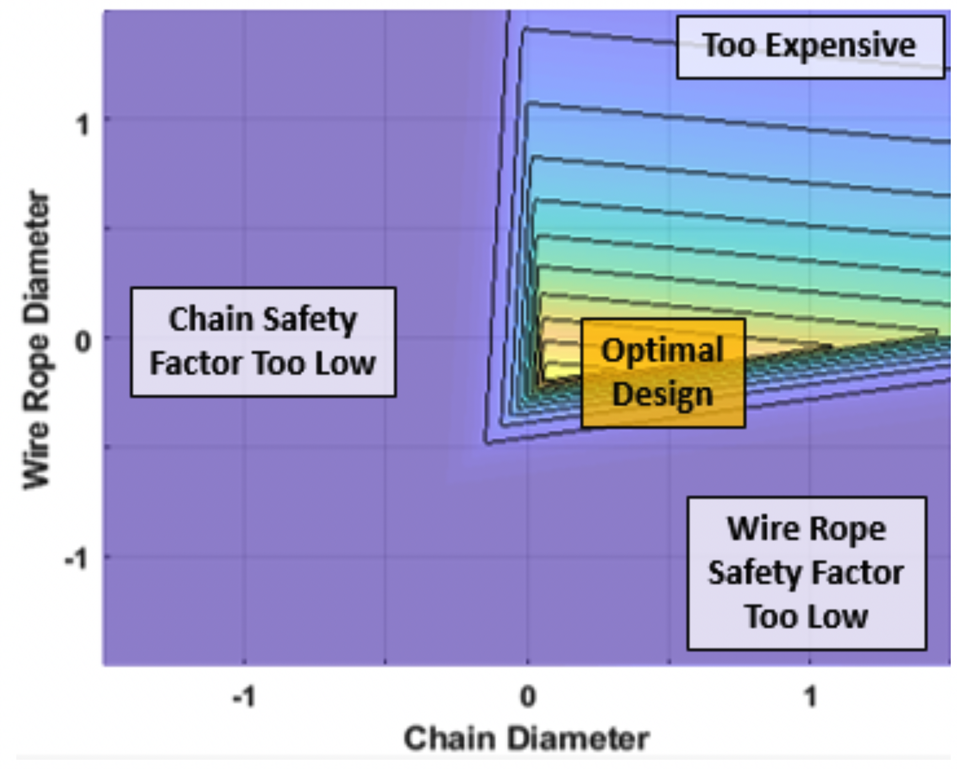
Fig. 7 shows the objective function as a surface plot with respect to the chain diameter and the wire rope diameter. There is a trade-off between safety factor and cost that suggests that the optimal wire rope and chain diameters are roughly halfway between the upper and lower DoE levels.
Figure 7 Objective surface plot shown with respect to chain diameter (x-axis) and wire rope diameter (y-axis). Yellow regions show the peak objective values.
Fig. 8 shows the objective function with respect to the buoy shape and size. The buoyancy must optimized to balance a reduction in cost with an increase in wire rope safety. As the buoyancy decreases, however, the ADCP pitch increases. An elliptical buoy shape better mitigates ADCP pitch than a spherical buoy.
Figure 8 Objective surface plot shown with respect to reserve buoyancy (buoy) shape (x-axis) and buoy volume (y-axis). Yellow regions show the peak objective values.
Fig. 9 shows the objective function with respect to the anchor mass and acoustic release buoyancy. The optimal design occurs when the anchor mass and acoustic release buoyancy are large, but beyond a certain point the design is less optimal as the cost of the system becomes the limiting factor.
Figure 9 Objective surface plot shown with respect to anchor mass (x-axis) and acoustic release buoyancy (y-axis). Yellow regions show the peak objective values.
III. Results
Once the objective function was defined, most standard optimization routines can be used to determine the optimal values. TABLE II. summarizes the optimal levels of each factor.
Table 2 Summary of Optimal Design
The optimal ADCP buoy is an elliptical buoy with a diameter of 50.5 inches. The optimal mooring lines are a 7.6 mm diameter wire rope and an 8.1 mm diameter studless chain. To ensure that sliding on the seabed is minimized, the anchor mass must be 1,694 kg, slightly larger than the highest level simulated. The acoustic release needs an additional 0.185 m^3 of buoyancy to ensure that it will be retrieved if it becomes separated from the buoy.
To validate that the DoE procedure successfully converged on a working arrangement, the design summarized in TABLE II. was simulated for a duration of three hours in the maximum 50-year return period sea state at the Jeffrey’s Ledge site. Extreme Value Analysis was used to find the peak expected value and confidence intervals for each objective. For objectives that are Gaussian, or nearly so, the three-hour extremes were computed according to:

Here x is an arbitrary data field, μx is the simulated mean, T is the dominant wave period, and σx is the simulated standard deviation.
For non-Gaussian distributed objectives, such as the mooring tension, the three-hour extremes were fit to a Generalized Pareto Distribution, using a Peaks-Over-Threshold (POT) approach [10], [11]. Then the upper 95th percentile of the expected values are used.
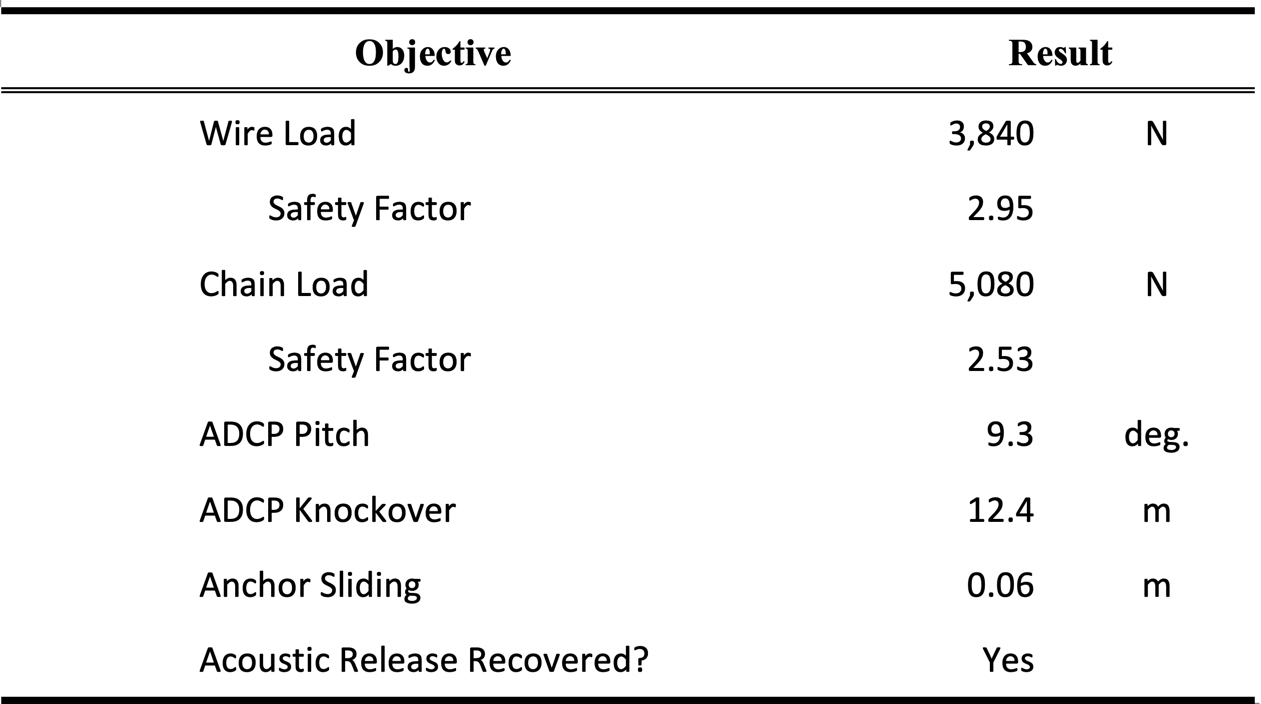
The results are summarized in TABLE III. The wire rope and chain safety factors are acceptable – both well above the target of 1.67 [7]. The pitch angle and knockover are manageable, the anchor stays in place, and the Acoustic Release is successfully recovered.
Table 3 Summary of Optimal Design Results
IV. Discussion
Maine Marine Composites, in collaboration with DeepWater Buoyancy Inc, applied a Design of Experiments-based simulation approach to developing a robust, cost-effective mooring system for a hypothetical submerged ADCP in the Gulf of Maine. The DoE approach made it possible to quickly examine a broad range of design factors and levels, and the optimal design was shown to meet all the desired objectives.
The objective function used for optimization is based on linear regression of the DoE results. The objective function is constructed in such a way that all objectives are met without needlessly maximizing any objectives beyond their target levels. This approach supports both constraints and objectives, where constraints are a limit the design must achieve (“Ensure that the mooring safety factor is at least 2.2”) and objectives are more open-ended (“Minimize the cost of the mooring system”).
References
- Fisher, R., Design of Experiments, 8th, Oliver and Boyd LTD, Edinburgh, 1960.
- Ma, B.B., Lien, R-C., and D.S. Ko, “The variability of internal tides in the Northern South China Sea,” J. Oceanogr. 69, 2013, pp. 619-630.
- National Oceanic and Atmospheric Administration’s National Data Buoy Center. “Station 44098 – Jeffrey’s Ledge, NH (160).” S. Dept. of Commerce. https://www.ndbc.noaa.gov/station_page.php?station=44098.
- Eckert-Gallup, Sallaberry, Dallman, Neary. “Application of principle component anlysis (PCA) and improved joint probability distribution to the inverse first-order reliability method (I-FORM) for predicting extreme sea states,” Ocean Engineerign, 2016, pp. 307-319.
- Coe, R.G. Michelen, C., Eckert-Gallup, A., Yu, Y., and J.v. Rij, “WDRT: A toolbox for design-response analysis of wave energy converters,” Proceedings of the 4th Marine Energy Technology Symposium (METS), Washington D.C., 2016.
- Haver, S., and S. Winterstein, “Environmental contour lines: a method for estimating long term extremes by short term anslysis,” Trans. Soc. Nav. Archit. Mar. Eng. 116, 2009, pp. 116-127.
- American Bureau of Shipping (ABS), Guide for Position Mooring Systems, Houston, TX, 2018.
- Krishnaiah, K., and P. Shahabudeen, Applied Design of Experiments and Taguchi Methods, PHI Learning Private Limited, New Dehli, 2012.
- Orcina LTC, OrcaFlex User Manual: OrcaFlex Version 10.2c, Daltongate Ulverston Cumbria, UK, 2018.
- Bommier, E., “Peaks-Over-Threshold Modelling of Environmental Data,” U.U.D.M. Project Report, 2014:33.
- do Nascimento, F.F., Gamerman, D., and H. Freitas Lopes, “A semiparametric Bayesian approach to extreme value estimation,” Stat. Comput. 22, 2012, pp. 661-675.
About DeepWater Buoyancy, Inc.
DeepWater Buoyancy creates subsea buoyancy products for leading companies in the oceanographic, seismic, survey, military and offshore oil & gas markets. Customers have relied on our products for over thirty-five years, from the ocean surface to depths exceeding six thousand meters.
Learn more at www.DeepWaterBuoyancy.com
About Maine Marine Composites
MMC specializes in motion prediction for ships and platforms, analyses of fluid/structural dynamics, and mooring system design and simulation. Our engineering staff has decades of experience with design and analysis of ships and offshore energy systems, and has successfully completed diverse and challenging projects for many of the most highly regarded offshore and ocean energy companies.
For more information, please contact Richard Akers at dakers@mainemarinecomposites.com
Learn more at www.mainemarinecomposites.com