Mooring Matters: StableMoor® Buoys in the Bay of Fundy
For the next installment in our series of technical articles, we look at the use of StableMoor® Mooring Buoys in a recent project by Ocean Tracking Network in the Bay of Fundy.
Project Summary
DeepWater Buoyancy and DASCO Equipment Inc. partnered with the Ocean Tracking Network (OTN) to execute a major upgrade to their mooring platform for monitoring equipment in the Bay of Fundy.
OTN, in partnership with Dalhousie University, has established an acoustic system to track aquatic animals in the Bay of Fundy. Specifically, the project aims to track the effects of tidal power installations in the upper Minas passage on the local marine environment and wildlife.
Mooring Equipment Challenges in the Bay of Fundy
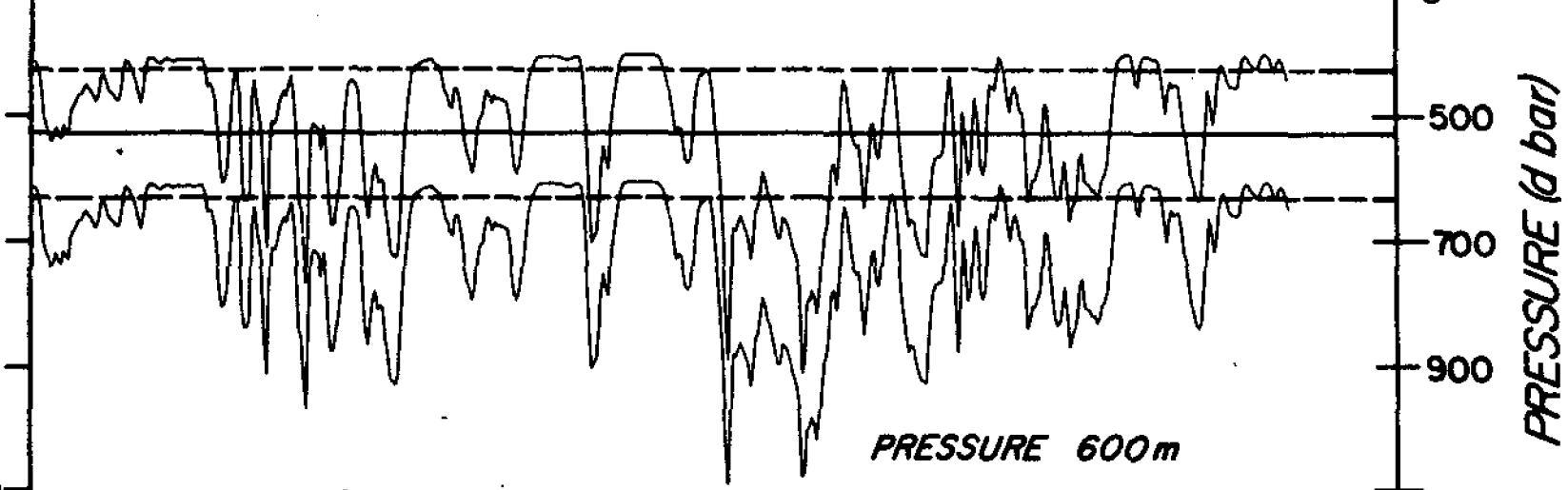
The Bay of Fundy is one of the world’s most dynamic bodies of water, due to its strong tidal currents. This makes it an ideal location for tidal power projects, but challenging for moorings.
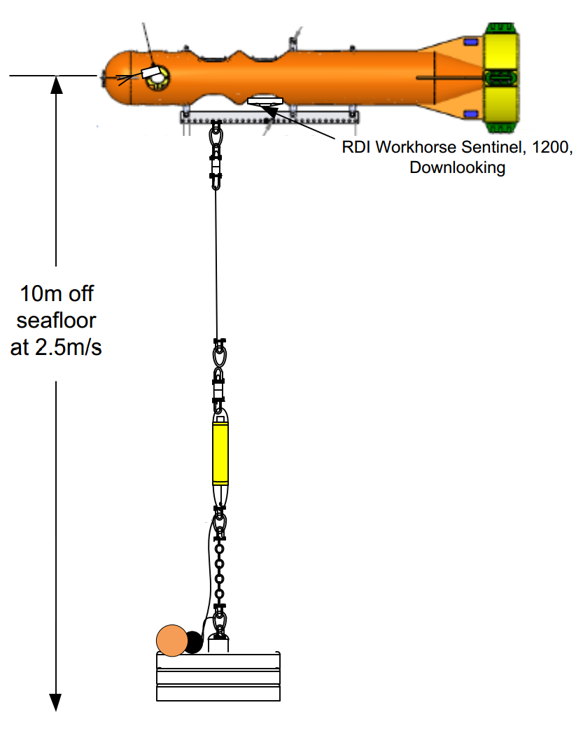
In 2010 OTN deployed a series of single point moorings with fish tracking technology. Over the next decade, the project faced numerous failures related to the mooring design such as equipment breakage, destruction of the mooring hardware leading to washups, and occasional entanglement with fishing gear. Additionally, the mooring required service every six months.
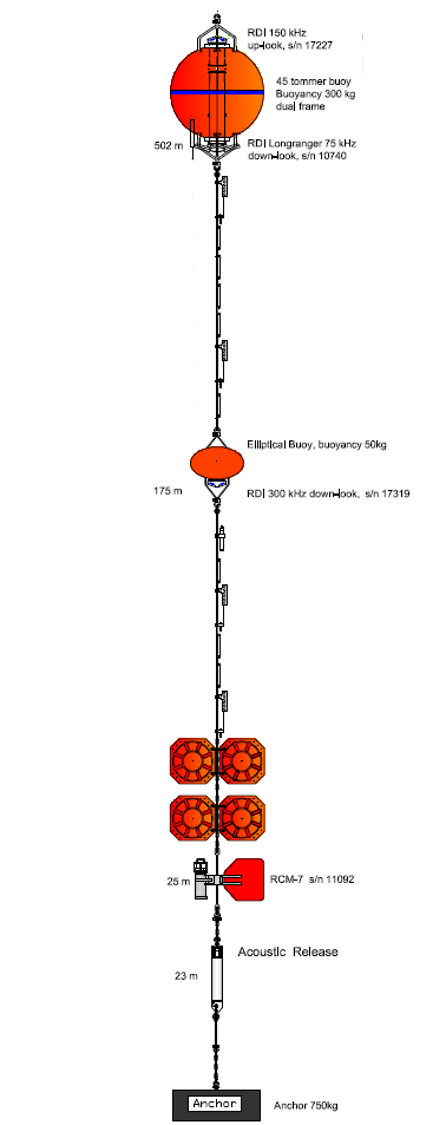
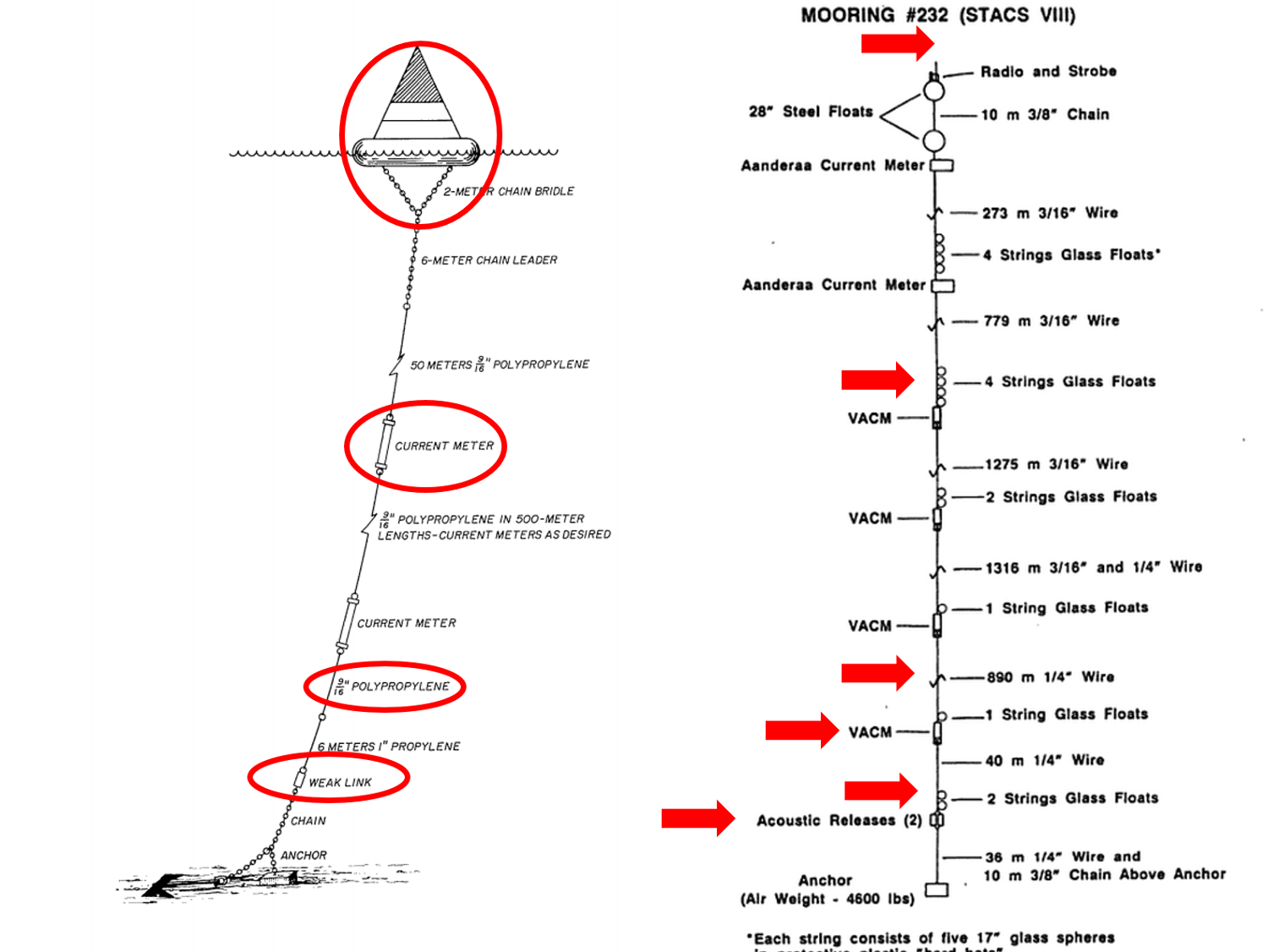
In 2023 OTN partnered with DeepWater Buoyancy and DASCO Equipment to redesign the mooring platform to reduce equipment issues and frequent servicing. A major component of that redesign included the use of a custom-built version of DeepWater Buoyancy’s StableMoor® Mooring Buoy.
Photos courtesy of Joseph Pratt, Ocean Tracking Network.
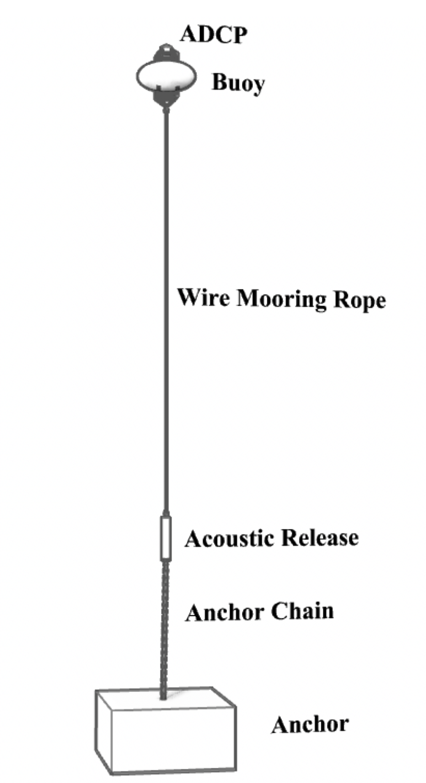
The moorings capitalized on the low coefficient of drag inherent in the StableMoor® design, as well as the robustness of the syntactic foam. Durable and corrosion-resistant stainless steel chains and shackles were utilized, and the bushings and plates updated to ensure functionality in the Bay of Fundy’s extremely dynamic tidal flow.
The mooring design changes significantly improved the performance and dramatically decreased the number of mooring failures.
Weathering the Bay of Fundy with Custom StableMoor® Buoys
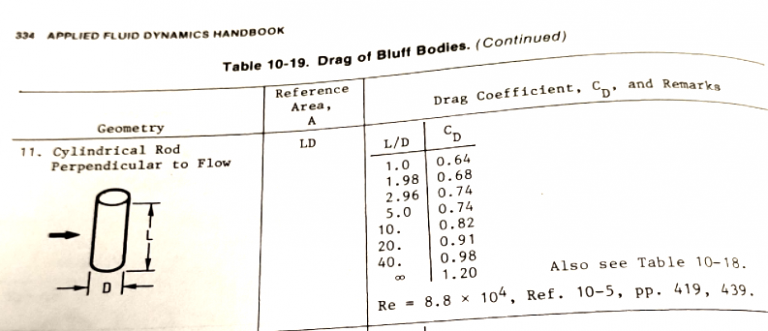
Specifically engineered for high current applications, the StableMoor® is designed to reduce drag and increase mooring stability in extreme flow regimes. By decreasing frontal area (compared to spherical buoys) and increasing dynamic stability in high current areas, the StableMoor® minimizes mooring inclination and excursions. The StableMoor® Mooring Buoy is the lowest drag instrument platform available on the market today.
To meet OTN’s specific needs for the Bay of Fundy monitoring project, DeepWater Buoyancy’s engineers created a smaller version of the design with custom instrument wells and hardware. To account for changes in current direction without excessive wear, 316L stainless steel mooring swivels were chosen. The stainless steel material also provides crucial durability in highly corrosive seawater.
DeepWater Buoyancy looks forward to working with OTN and DASCO to modify and perfect the monitoring platform.
What’s Next?
In 2024 another round of improvements is planned. One of the goals of the exercise is to extend the mooring’s battery life to one year, thus reducing service frequency. The plans will also investigate equipment to allow retrieval of the anchors, which are currently left on the seafloor when the moorings are recovered.
“DeepWater Buoyancy is excited to work with our long-term partners, DASCO and the team at the Ocean Tracking Network on such important work.”, said Dan Cote, Sales Manager.
What the Ocean Tracking Network Does
Headquartered at Dalhousie University in Halifax, N.S., OTN has established an acoustic system to track aquatic animals in the Bay of Fundy. Specifically, the project aims to track the effects of tidal power installations in the upper Minas Passage on the local marine environment and wildlife.
OTN is a science, data management and partnership platform that supports research collaborations in freshwater and ocean locations across the globe. In the Bay of Fundy, OTN and its collaborators have been an integral part of monitoring fish-turbine interactions near OpenHydro turbines.
Using specialized equipment, they monitor the movements, behaviors, and environmental preferences of fish and other aquatic species. Knowledge generated through OTN collaborations is used by scientists, managers, policymakers, industry, and Indigenous and coastal communities to conserve and manage shared resources.
About DASCO Equipment
DASCO Equipment is Canada’s leader in oceanographic, hydrometric & marine survey technologies. The company’s primary business is the sales, and sales support, of this equipment, however, they also maintain a large pool of rental equipment, including acoustic doppler current profilers, multibeam and single beam echosounders, marine GPS and GNSS systems and marine survey software packages.
Learn more at www.dascoei.ca.
About DeepWater Buoyancy, Inc.
DeepWater Buoyancy, Inc., located in Maine USA, provides subsea buoyancy products for offshore energy, oceanographic, military, and technology companies around the world. Customers have relied on our products for over forty years, from the ocean surface to depths exceeding six thousand meters. Learn more at DeepWaterBuoyancy.com